• színek

A szimmetria

Környezetünkben körülnézve szinte mindenütt a formákon szabá­lyos elrendezettséget látunk. Ezek az elrendeződések valamilyen szabályos rendben folynak, valamilyen formai ritmikusságot, peri­odicitást, ciklikusságot, ismétlődést, analógiát, homológiát, foko­zatosságot, hierarchikusságot, szimmetrikusságot és egyebeket tapasztalhatunk. A szabályos formai rendszerek között legáltalá­nosabban elterjedt a szimmetria, amit a mindennapi szóhaszná­latban is igen gyakorta alkalmazunk.

A szó görög eredetű, jelentése „együttes mérés, összemérés, helyes arány”. Aszimmetria a görög matematikában összemérhetőséget jelent, pontosabban fogalmazva két vagy több mennyiségnek egész számokkal kifejezhető arányát. Később már az arányrendszerek is használták ezt a fogalmat. A 18. századtól az azonos (egyformaság, egybevágás) részek megfelelését, ki­egyensúlyozottságát értjük rajta. Szimmetrikus például az egyforma részekre bontható sík vagy az egyenlő részekre osztható test. Manapság általában a tükörszimmetriát értik alatta. A különböző tudományterületek a szimmetria fogalmán a maguk szimmetriatípusainak meghatározását értették, amelyeket definiáltak, és elnevezéseikben specifikáltak.

Nemcsak a tudományok területén ismeretes ez a fogalom, hanem a művé­szetek területén is: a képzőművészetben, az irodalomban, a zenében. Ha egy műalkotást szimmetrikusnak minősítünk, ezzel azt fogalmazzuk meg, hogy a felezőtengely két, pontosan egymásnak megfelelő részre bontja az egészet. Ez a tagolás mozdulatlanságot, állandóságot fejez ki, s ennek érzetét váltja ki a nézőből, vers vagy zenei előadás alkalmával a hallgatóból.

A következőkben a szimmetria vizuális megjelenéseivel ismer­kedhetünk meg. A szimmetria esztétikai megfogalmazás szerint a műalkotás részének szabályszerű elrendeződése, amelyben minden ponthoz hozzátartozik egy neki megfelelő másik pont. Az esztétika kezdet­től fogva a szépség, művésziesség kritériumának tartotta. A szimmetriarendszereket a szimmetriatagok, szimmetria­elemek, szimmetriaszerkezetek hozzák létre, amelyek egyszerű (alap) szimmetriákba vagy összetett szimmetriákba rendeződhet­nek síkban és/vagy térben.

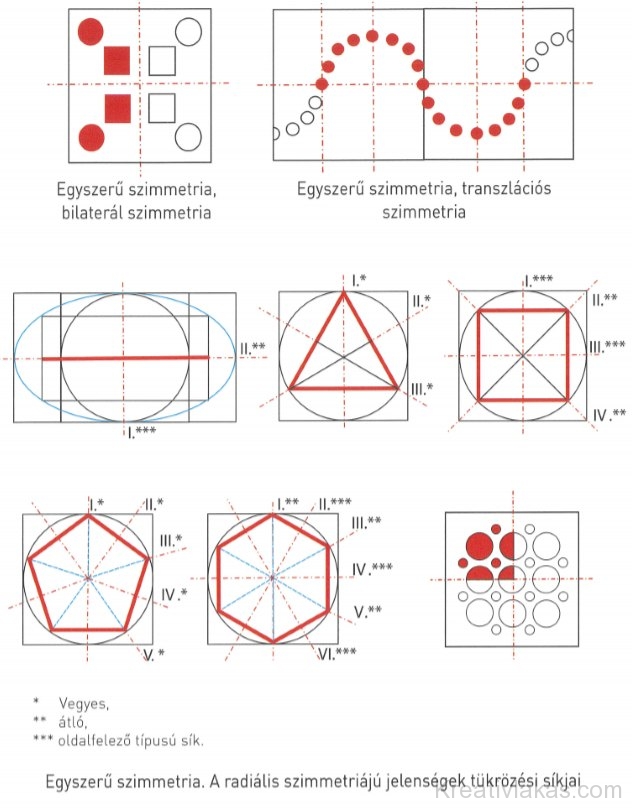
Egyszerű szimmetriák (kétdimenziós elrendeződések)

Bilaterális szimmetria. „Tükör-, hátoldali, jobb-bal oldali szimmetria”. A transzformáció a tükröződésen alapul, szimmetriaeleme a tükörsík, szimmetriatagja a tükrözött fél.

Transzlációs szimmetria. „Szalag- vagy láncszimmetria”. A transzformáció az eltolódáson alapul, szimmetriaeleme a transzformációs tengely, szimmetriatagja a metamer (monomer transzlációs változata) általánosításban.

Szín, forma tengelyre rendezett kapcsolatai. A szimmetriatengely mentén az ismétlődő formák irányultsága szabályozza, meghatározza az egyes szín- és formacsoportok létrejöttét

Radiális szimmetria. „Sugaras vagy forgási szimmetria”. A transzformáció a forgatáson (rotáción) alapul, szimmetriaeleme a forgástengely, szimmetriatagja azonos szimmetrikus jelenséggel együtt jelen lévő altaggal közösen kerülnek elforgatásra. A pá­ros számú tükröződésű síkkal rendelkező, radiális szimmetriájú rendszerekben a tükröződési síkok lehetnek átlós vagy oldalfelező típusúak.

Antiszimmetria. „Poláris vagy középpontos szimmetria”. A transzformáció a forgatáson (rotáción) alapul, szimmetriaeleme a forgástengely, szimmetriatagja azonos szimmetrikus jelenséggel együtt jelen lévő altaggal közösen kerülnek elforgatásra. A páros számú tükröződésű síkkal rendelkező, radiális szimmetriájú rendszerekben a tükröződési síkok lehetnek átlós vagy oldalfelező típusúak.

Komparatív szimmetria. „Hasonlósági szimmetria”. A szimmetriatagok egyformaságuk mellett bizonyos vonatkozásokban eltérnek. A transzformáció a modifikáción (átalakuláson, módosuláson) alapul. Szimmetriaeleme ismeretlen, míg szimmetriatagjai az egyes hasonló elemek egységes ismétlődéséből jönnek létre. A transzformáció létrejöttének bármely pontja hasonló bármely másik pontjához. A kiindulópontok és irányok között nincs belső összefüggés.

Homotrop szimmetria. „Ideális szimmetria”. A transzformá­ció létrejöttének bármely pontja hasonló bármely másik pontjához. A kiindulópontok és irányok között nincs belső összefüggés.

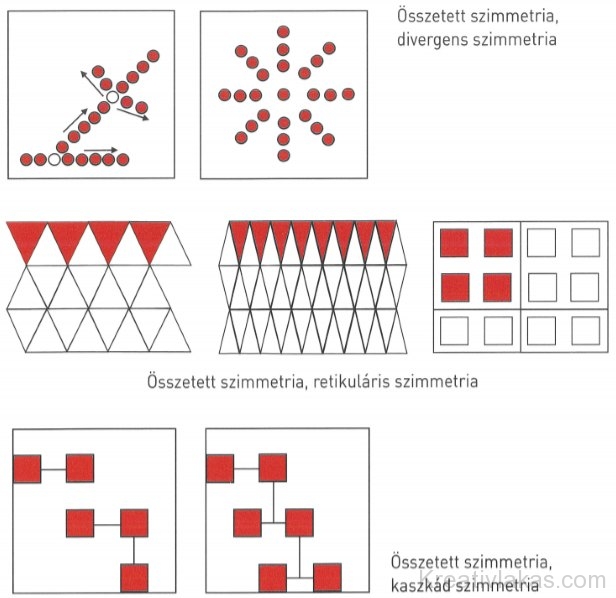
Összetett szimmetriák (három- vagy többdimenziós elrendeződések)

Az összetett szimmetriák igen sok félék Lehetnek, a szimmetriái elemek elrendeződése síkban, térben, tér-időben egyaránt létrejö­het, ebből adódóan nagyon sok féle változat lehetséges, amelyek­ből csupán néhány mintázat bemutatására van most lehetőség.

• Az összetett szimmetriájú rendszerek szerkezetét illetőleg legalább két különböző szimmetriaelem és transzformáció szüksé
• Az összetett szimmetriájú rendszereket megkülönböztethet­jük aszerint is, hogy a rendszerben részt vevő szimmetriaele­mek és a hozzájuk tartozó transzformációk típusa mennyiben azonos vagy mennyiben különböző, ami szerint lehetnek egy­nemű (homonóm) és különnemű (heteronóm) összetételűek, síkbeli és térbeli elrendeződésűek.

Divergens szimmetria vagy „elágazó szimmetria”. Kétszeres vagy többszörös transzformációval létrejövő Egysze­rű transzformáció esetén egyes szimmetriatagjaira külön-külön újabb transzformáció jön létre. A transzformációs tengelyek egye­nes síkban síkbeli rendszert eredményeznek, míg a különböző irá­nyú kiterjedésben térbeli rendszereket hoznak létre. Mind a sík-, mind a térrendszerek mint transzformációs folyamatok magukban foglalják az idődimenziót is. Egyes transzformációs folyamatokban a térdimenziók, míg másokban az idődimenzió a domináns meg­határozó tényező. Minden transzformációhoz azonos értékű szim­metriatagok tartoznak.

Retikuláris szimmetria. A transzformáció homonóm össze­tételű, és két vagy több transzformáció révén jön lé Ellentétben a divergens szimmetriával, itt minden transzlációhoz a megfelelő transzformáció során létrejött teljes szimmetrikus rendszer tartozik mint szimmetriatag. A transzformációk száma meghatározott: 1, 2, 3 vagy A lehet a téridő négy dimenziója mentén. Egyetlen transzfor­máció csak határesetként létrejövő retikuláris szimmetria (valójá­ban megfelel az egyszerű transzlációs szimmetriának, lánc, szalag jellegű). A két dimenzió mentén létrejött síkháló-, rács-, a három dimenzió mentén létrejött pedig térháló- vagy térrács-szimmetriák. Negyedik dimenzió (idő) mentén történő transzláció mint időbeli lé­tezés. Elméletileg négynél több transzláció is lehetséges, ami csu­pán matematikailag írható le.

Szferikus szimmetria vagy „gömbszimmetria”. Tökéletes szimmetriaként is nevezik, amely homonóm összetételű, két egy­másra merőleges, végtelen rendű forgástengelyen történő ismét­lődés eredmé Közömbös, hogy milyen a kiinduló szimmetria­tag alakja, szerkezete, valamint hogy milyen térbeli viszony van a kiinduló szimmetriatag és a két forgási tengely között, az ered­mény a gömbszimmetria létrejötte.

Ciklikus szimmetria vagy „ismétlődő szimmetria”. A kiindu­ló, nyitott szimmetriatag minőségileg megegyezik a végsővel, azaz a zárótaggal, így a folyamat végtetenítve ismétlő A nyitótag tetszés szerint kiválasztható, a ciklikusságban bárhol belépve a ciklusra jellemző számú transzformáció után a belépési helyre ju­tunk vissza. A ciklikusság lehet állandó vagy folyamatosan bővülő formáció.

Helikális szimmetria vagy „csavarszimmetria. A csavar­vonal-szimmetria lehet homonóm vagy heteronóm, amelyek a hozzájuk tartozó transzformációk kombinációjában különbö A homonóm (egynemű) rotáció is transzláció eredménye, a radiális és a transzlációs szimmetria kombinációja. Szimmetriatagjai csak a tér-idő koordinátáiban térnek el egymástól. A heteronóm (külön­nemű) rotáció a modifikációés a transzláció, azaz a ciklikus és a transzlációs szimmetria kombinációja. Mindkét esetben a szim­metriatengelyek párhuzamosak, az elemi transzformációk minden egyes szimmetriatagra hatnak, és felváltva működnek.

Spirálszimmetria vagy „csavarvonal-szimmetria”. Tekint­hetünk egy kúp palástjára vagy gömbfelületére illeszkedő, csa­varodó spirálvonalat, vagy egy hengerpalást felületére illeszke­dő, csavarodó spirálvonalat, amelynek a síkbeli vetülete egy kö A spirálszimmetriákat részben megkülönböztethetjük homonóm és heteronóm alaptípusok alapján, másrészt a sík- és térspirál, illetve a két-két alaptípus kombinációi alapján.

Kaszkád szimmetria vagy „lépcsős szimmetria”. Szin­tén lehet homonóm vagy heteronóm szimmetriatranszformáció. A homonóm kaszkád szimmetria lehet két, egymással szöget be­záró tengely mentén történő váltakozó transzláció, ahol a szim­metriatagok azonosak. A heteronóm kaszkád szimmetria szintén két csoportra osztható: az identikusra és differensre, melyeket most nem részletezünk.

Az aszimmetria

Aszimmetrikusnak nevezzük azokat a jelenségeket, amelyek az eddig említettekkel szemben a valós transzformációkra nemszimmetrikusak. Aszimmetrián a részek egyenlőtlenségét értjük. Ez a fajta tagolás a mozgás érzetét váltja ki, hiszen külön­böző időmennyiséget kíván a részek szemlélése vagy hallgatása. A mozgó, fejlődő, eleven dolgokat dinamikusnak nevezzük. Az aszimmetria helyett dinamikát, az aszimmetrikus helyett dinami­kust mondunk a különböző nagyságú részekből komponált alko­tások jellemzésére. A 20. századi művészet mint, zene, festészet, nonfiguratív szobrászat, egyik fő tendenciája az aszimmetriára való komponálás.

Diszimmetriának nevezzük azt a „pontatlanságot”, amely valójában minden szimmetriatípusban jelen van. Tökéletes szimmetria ugyanis valójában nem létezik, mert minden létező szimmetrikus jelenség szimmetrikussága kisebb-nagyobb mér­tékben pontatlan.