• növények
• színek

Arányok a természetben és az építészetben

A művészetekben megjelenő arány az adott kor világképének tük­re. A reneszánsz tökéletes aránya kozmikus szépséget fejez ki, a legdrámaibb, legdinamikusabb, legfeszültebb arány harmóniába fogja a szimmetriát és az aszimmetriát, amely a humanista művé­szet egyik legfontosabb alapeleme.

Az „isteni” arány

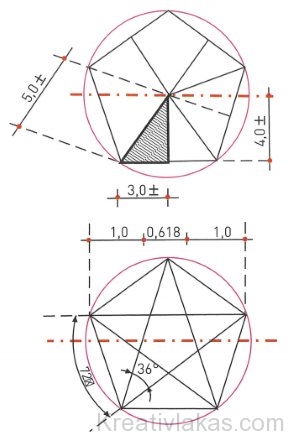
Az isteni arány (divina promortione), az isteni metszet (sectio divina), másképpen az aranymetszés (sectio aurea) egy sajátos, ki­tüntetett rangú arány. Első meghatározását Eukleidész geometriai tankönyvéből ismerjük: a:b = b:(a+b). A körzővel, vonalzóval való szerkesztési módját a Kr. e. 5. és 6. század görög matematikusai már ismerték.

Pitagoraszi aranymetszés

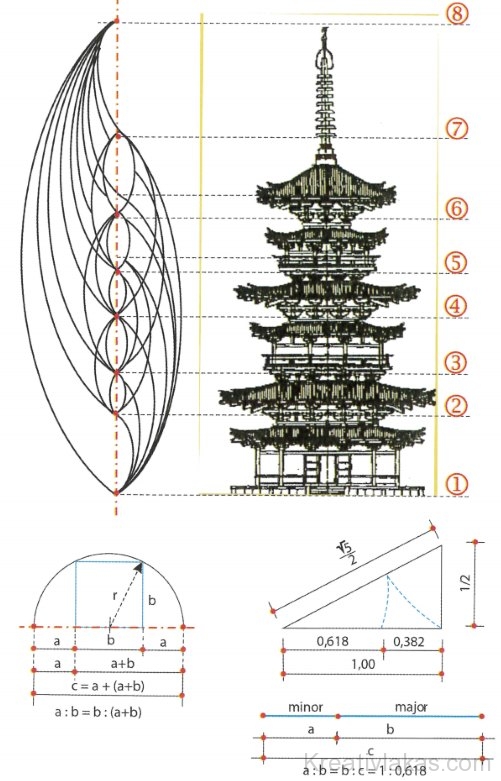
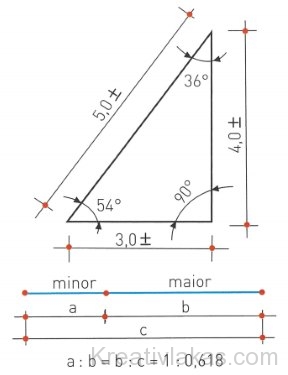A kisebb (minor) rész úgy aránylik a nagyobb (maior) részhez, mint a nagyobb rész az egészhez

Az aranymetszés aránya

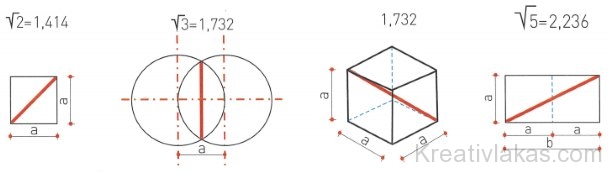
A „filozófus” szó megalkotója, Pitagorasz (Püthagorasz) úgy gondolta, hogy a matematika és a hozzá kapcsolódó tárgyak tanulmányozása kiemelkedően fontos, mivel ezek a tanulmányok feltárják az univerzum belső működését. Pitagorasz szerint a számok tudománya mindennek az alapja. A számok mindegyike egy-egy univerzális rezgés esszenciája: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Pitagorasz azt is felfedezte, hogy a 2, 3, 5 számok négyzetes gyöke olyan alapvető minőségek, amelyek a teremtés minden formájában jelen vannak.

• Aritmetika: szám önmagában.
• Geometria: szám a térben (eredeti jelentése: „megméri a Földet”).
• Zene: szám az időben.
• Asztronómia: szám a térben és időben.

Csodatévő ábrát láttak benne a bölcsek, papok, varázslók is, akik az aranymet­szésről soha nem is hallottak. Kepler (1571-1630) hívő szellemben magasztalta a „sectio divina”, az isteni metszet szerepét: „Ez a mértani arány lehetett, úgy vélem, a teremtő ideája, a hasonlónak hasonlóból való nemződések bevezetése. A bibliai eredetű, Dávid-csillagnak nevezett zsidó szimbólum két, egymásba forduló szabályos háromszögből kirajzolódó hexagram. A 17. századi prágai zsi­dó közösség tagjai számára lett megkülönböztető jel a sárga csillag. Pontosan ilyen hatszögű csillagot öntöttek rézbe Amerikában is, hogy a seriffek hivatali jelvénye legyen. A forma azonos, de a két tartalomnak nincs köze egymáshoz.

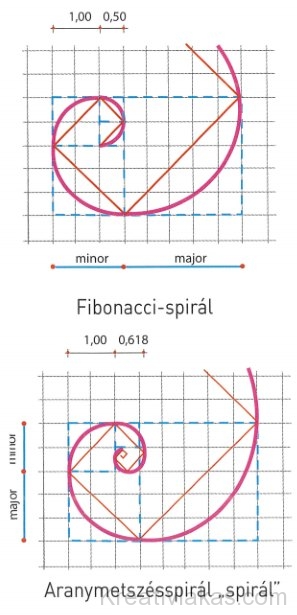
A 13. században a „pisai Leonardo”, Bonacci fia, ismert nevén Fibonacci (1 170-1250) diplomataként tett nagy utakat Egyiptomban és Szíriában, így volt lehetősége megismerkedni az arabok magas színvonalú matematikájával. „Liber Abaci” c. értekezésében foglalta össze fejtegetéseit. Híres sorozata egy számtani sor, 1, 1, 2, 3, 5, 8, 13, amelyben minden számot az előző kettő össze­geként kapunk meg. 1 + 1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13. Különlegessége, hogy a számok növekedésével két egymás melletti elem aránya egyre jobban közelít az aranymetszés arányához.

Ahogy később látni fogjuk, az aranymetszés aránya a képzőművészetben és az építészetben is különleges szerepet kapott. Ennek az az oka, hogy a termé­szetben is számtalan helyen és formában megnyilvánul ez a különleges arány. A görög költők többször is említik a bor és a víz keverésénél a 2:1, 3:2, 5:3 arány­párt, tehát ismerték a törvényszerűséget, a „Fibonacci-számsort”.

Arányok a természetben

A több mint 250 évvel Leonardo da Vinci előtt élt Leonardo Fibo­nacci személyének köszönhetően tárult fel előttünk az a csodála­tos világ, amit a természetben megfigyelt. A virágok szirmainak, leveleinek, a növények magjainak nume­rikus törvényszerűségeit sokan vizsgálták és kutatják ma is.

Csigák

Napraforgó szerkezeti rajza, amelyben az aranymetszésspirál érvényesül

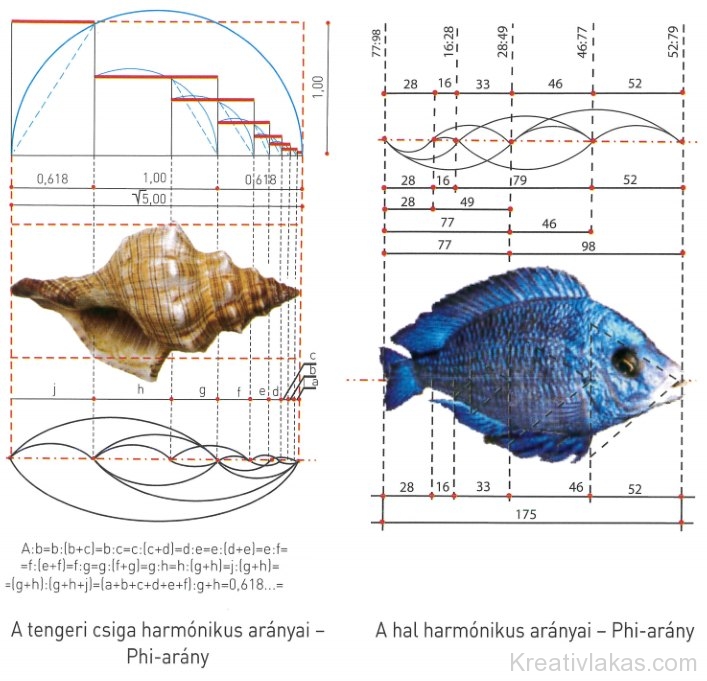
R. Engel-Hardt könyvtörténész a könyvformátumok tervezéséhez is az arany­metszésben látta a „tökéletes arányt”. A növényekről jelentős megfigyeléseken és méréseken alapuló megállapításokat tett. 60 tölgyfáról összesen 500, min­den külső erőszaktól mentes levelet gyűjtött össze, és arra a következtetésre jutott, hogy közülük 235 pontosan megfelel az aranymetszés szabályainak, míg a többi csupán néhány milliméterrel tér el attól. Számszerűen kifejezve a leve­lek hosszúságának és a szélességének az aránya, a függőleges tengelynek a kereszttengelyhez való aránya 8:5 vagy 5:3. Bár ezekből a mérésekből általános következtetést nem vonhatunk le, érdemes idézni O. Hagenmaier idevonatkozó gondolatait.

„Semmiképpen sem szabad azt állítani ezek a méretarányok minden esetben előfordulnak a természetben csak azt, hogy a természet is ismét és ismét ugyanezekre törekszik. Túl messzire mennénk, ha az aranymetszést természeti normának értelmeznénk. Az világos, hogy nem az ember eszelte ki az arany­metszést, hanem bizonyos értelemben a természet dolgozik e szerint. A ter­mészeti viszonyok néhány példáján felismerhetjük, hogy az ember az uralkodó méretarányokat elleste és a pentagrammban találta meg hozzájuk a kulcsot.”

A phi-arány többi között megjelenhet az élőlények méreteinek hosszúsági arányaként, vagy a phi-arányszám felhasználásával szerkesztett spirál formájában is.

Arány az építészetben

Az arány minden építészeti mű alapvető elvi alkotóeleme. Most csak néhány példát említünk a különböző arányelvek alkalmazá­sára a világ építészetéből.

Athén Akropoliszán fenségesen tekint a Parthenon még ma is az alatta elterülő városra. A görög építészet nemcsak a maga ide­jében, hanem máig csodálattal tölti el azt, aki szemtől-szemben találkozik a látvánnyal. Lenyűgöz minket a helyszín-méretarány­tömeg funkció tökéletes egységével. A görög építészet híres arról, hogy az aranymetszés arányára törekedtek. Az arány azonban nem az épületek méreteiben mutatkozik meg, hanem annak látványá­ban: a perspektivikus rövidülések hatását korrigálták az arány mi­nél tökéletesebb megjelenése érdekében.

Leon Battista Alberti az új mértékegység (exempeda) megsok­szorozásának elve szerint az aritmetikai (egész) számokat viszo­nyító szerkesztés szabályát kutatta. Az emberi arányokat az épü­letek és épületrészek arányaival azonosította, így demonstrálta az emberi test architektonikus szimmetriáját, és egyben az építészet antropomorf életteliségét.

Alberti szerint a részek harmóniája három tényezőtől függ: numerus (szám), finitio (arányosítás] és colocatio (csoportosítás) együttesen teremtik meg a concinitast, az összhangot. A görög filozófiából eredő, majd Vitruvius által az építészetre alkalmazott alapszabály szerint a szépség az összes részek harmó­niája, amiből ha bármit elveszünk, csorbát szenved az együttes tökélye. A rene­szánsz építészetben az arány alapvető, matematikailag biztosított kompozíciós törvénynek számított.

„Rend nélkül semmi sem lehet szép, kényelmes vagy örö­met keltő.” „A zenei arányok építészeti alkalmazása közvetlenül alkalmazható a természet harmóniatörvényeihez. A természetet elvontabb formákra bontva, elvontabb arányosságok következnek, a négyzet és a háromszög variációinak a zenei összhanggal történő egyesítése, a középarányosok téralakító lehetősége alapján” (Leon Battista Alberti).

Alberti építészetében az oszloprendet tartja az építészet legne­mesebb részének, ezért szívesen alkalmazza a lakóházak homlok­zatán annak ellenére, hogy az antik építészetben ez nem volt jelentősen elterjedt. Alberti tervei nyomán készítették el Firenzében a 13. században a Santa Maria Novella háromhajós, bazilikális belső elrendezésű templom főhomlokzatát. A terv alapjául az oktáv zenei arányának egyszerű geometrikus áttétele szolgált, vagyis a négy­zetes elrendezés.

A teljes homlokzat 35 m oldalméretű négyzetbe foglalható. A vízszintes felezővonal kijelöli az alsó rész magasságát. A nagy négyzet oldalhosszának felével képzett négyzet így kétszer mérhe­tő rá az alsó szakaszra, felül pedig pontosan befoglalja a kiemelt középrészt. A négyzetek további felezése és az átlók a homlokzat minden kompozíciós egységét meghatározzák. Az 1:2 arány a leg­kisebb részleteknél is pontosan alkalmazott. Az alsó rész alaprit­musát a sávozott törzsű sarokpillérek és a négy korinthoszi oszlop határozzák meg.

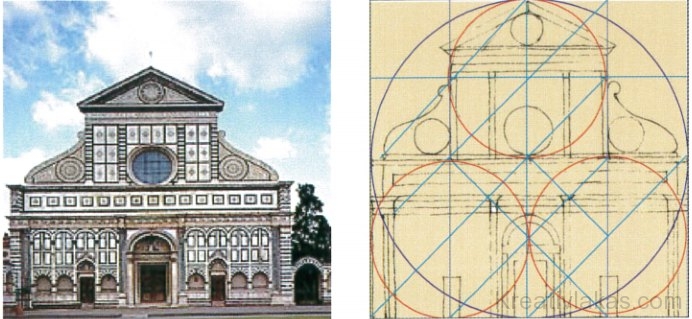Firenze: Santa Maria Novella homlokzatának négyzetes szerkesztése
M=1:2 arányban, az oktáv zenei arányának geometriai áttétele.

Santa Maria della Pace kolostorudvar építése közben, valami­vel 1 500 után tervezte Bramante a Tempietto néven ismert kör­templomot, amelyet néhány évvel később fel is építettek. A kis emléképület méretét megszabta a rendeltetése, mivel a „mártíriumkápolnába” csak a szertartást végző papok léphettek be. A hívek a nyitott ajtón keresztül, az udvarból követhették a szer­tartást (az egyiptomi és az antik görög kultúrából ismeretes ez a kettéválasztás).

Az arányok meghatározott rendszere különböző kultúrkörök gondolati összefüggéseiben is jelen van. Japánban is régóta léte­zik egy modul alapú arányosítási rendszer, amelynek alapegysége a tatami. Ennek tanulmányozása a mai modern építészet, design és kézműves iparművészet művelőinek is hasznos, a szemléletfor­málás érdekében.

A japán házak berendezése a Heian-kor végéig minimális volt. A magasított fa-padozatot feltekerhető, 5-6 cm vastagságú gyékényszőnyeggel, tatamival bo­rították, alváshoz is ezt használták, de akkor vattázott paplanfélével terítették le, és fejtámaszt is használtak. Ezen a fontos bútoron kívül a berendezést egy beépített polcos szekrényke, faszénégetésre szolgáló melegítő, valamint egy ivásra szolgáló kicsiny asztalka, és végül egy kis teázóasztalka jelentette. A ház belső tereit rizspapírral bevont, lakkozott, fakeretes válaszfalak választották el. A térelválasztó elemek vájatokban elmozdíthatók, szükség szerint kiemelhetők, így a belső terek tetszés szerint egybenyithatok, elhatárolhatók, bővíthetők, kü­lönféle térhasználati funkciókhoz igazíthatók.

Le Corbusier (1878-1957) a 20. század egyik legnagyobb építésze,éppen az em­beri méretek tanulmányozása révén vált az aranymetszés hívévé.1950-ben jelent meg az arányrendszerről szóló könyve, a „Modulor”. Az építész ebben azt kereste, hogy mi az a mértékrendszer, amely a legpontosabban követi az emberi mértéket. Le Corbusier a modulor-méretrendszerhez egy 183 cm magasságú, felemelt karú embert választott. „Elhelyezkedésének főbb pontjaiban, a láb, köldök, fej, felemelt kar ujjainak hegye három intervallumot szolgáltat, amelyek egy sor aranymetszést hoznak létre, s amelyeket a Fibonacci-sor szerint jelöltet.”

Le Corbusier: modulrendszer arányosítása. „Egységes halmazállapotot teremt, amelyet strukturálisnak is nevezhetünk. Az épület valamennyi külső falát, belső tereket, padlókat, mennyezeteket, falfelületeket – egészen a legkisebb részletekig – a méretek összefüggése határozza meg, és minden nézet, következésképpen minden élmény egymással kapcsolatban áll”

A modulor-mértékszámok az emberi alapmozgások és tevékenységek méreteit is magukban foglalják. így az alacsony ülésből kiindulva, amely 27 cm, az ülés­magasságot, vagyis a szék magasságát 43 cm-ben, a munkaasztal magasságát 70 cm-ben, míg a pult magasságát 86 cm-ben határozza meg. A polcmagassá­gokat 113, 140, 183 cm-es osztások jelölik, míg végül a minimális térmagassá­got 226 cm-ben irányozza meg.

A 20. század esztétikai indítékai, arányosítási törekvései is je­lentősek

Az op-art művészet kimagasló képviselője, a magyar származású Victor Vasarely (Vásárhelyi Viktor) 1970-ben megje­lent „A színes város” c. könyvében a színforma kettős plasztikai egységkénti felfogását hangsúlyozza.

Szerinte „az egység már önmagában is szép. Az érzelem legegyszerűbb formá­ját képviseli. De csupán külső megjelenése és arányai, a színek megválasztása és erőssége, végül más egységekkel való kombinálása révén nyeri el azt a töl­tést, amellyel érzékszerveinkre, majd értelmünkre hatást gyakorol. A szín-for­ma egységek mindegyike arányosan szűkíthető-tágítható, ami a nagyságrendek egész skáláját mint egy kompozíció mozgóléptékét eredményezi.” Vasarely szerint ez a „szín-forma egység” a 20. század új plasztikai nyelvének alapja, a „harmóniák és serkentő ingerek tárháza”, amely lefordítható a tech­nika nyelvére.

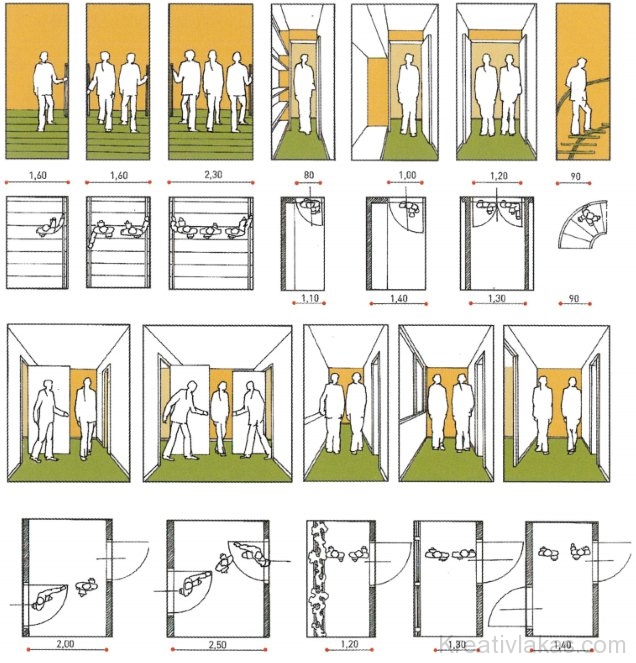
Belső térben történő közlekedés helyigénye (kép fent).
Antropometriai mérések:
Statikus antropometria: az egyes testrészek méreteivel foglalkozik, a megfelelően rögzített végtagoknál (pl. álló test mellé szorított karok) azért, hogy összevethetők legyenek máshol felvett méretekkel, ún. mérőpontokat állapítottak meg.
Dinamikus antropometria: nemcsak a mérésekkel, hanem az egyes testrészek által leírt mozgásokkal is foglalkozik (a még elvégezhető, és a kényelmesen elvégezhető mozgásokkal).